コレクション y=x^2 parabola 658551-Y=2x-x^2 graph
The curve y 2 = x represents a parabola rotated 90° to the right We actually have 2 functions, y = √ x (the top half of the parabola);Graph the parabola, y =x^21 by finding the turning point and using a table to find values for x and y The coefficient of the #color(green)(x^2# term is Positive and hence, our Parabola Opens Upward, and it has a minimum Please refer to the image of the graph below to verify our solutions The Axis of symmetry of a parabola is a vertical line that divides the parabola into two congruentWe can find the x intercept, y intercept, vertex, focus, directrix, axis of symmetry using any parabola equation in the form of y = ax 2 bx c In the following sections, we are providing the simple steps to find all those parameters of parabola equation
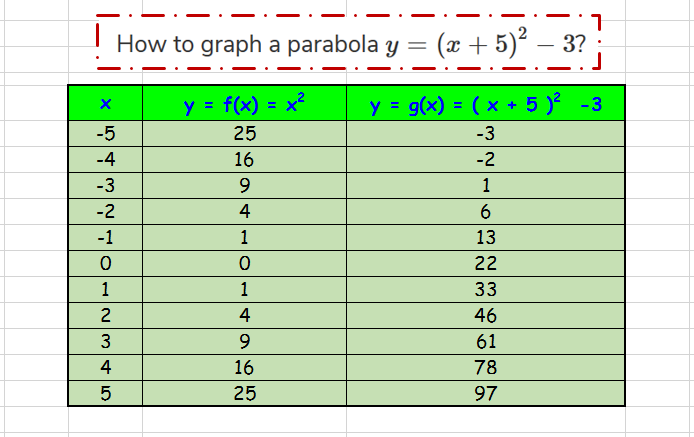
How To Graph A Parabola Y X 5 2 3 Socratic
Y=2x-x^2 graph
Y=2x-x^2 graph-Answer (1 of 9) Yes A parabola is the set of points equidistant to a given point (the focus) and straight line (the directrix) The curve x=y^2 is a parabola with a whose focus is (\frac{1}{4},0) and directrix is x = \frac{1}{4}Step 1 Solve for the vertex of the parabola The vertex of a parabola of the form {eq}y= x^2 bx c {/eq} is always given by {eq}\left (\dfrac {b} {2a},f (\dfrac {b} {2a})\right) {/eq} Step



Solution Graph Y X 2 1 Label The Vertex And The Axis Of Symmetry And Tell Whether The Parabola Opens Upward Or Downward
Graph the parabola given by the equation {eq}y=(x2)^23 {/eq} Step 1 Comparing the equation to the general vertex form {eq}y=a(xh)^2k {/eq} of aConsider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axisWe also get a parabola when we slice through a cone (the slice must be parallel to the side of the cone) So the parabola is a conic section (a section of a cone) Equations The simplest equation for a parabola is y = x2 Turned on its side it becomes y2 = x (or y = √x for just the top half) A little more generally y 2 = 4ax
Y 2 = 8x;X 2 = 16y ;Directrix y = 2 = 0 For horizontal parabolas, the vertex is x = a (y k)2 h, where (h,k) is the vertex The focus of parabolas in this form have a focus located at ( h , k) and a directrix at x = h The axis of symmetry is located at y = k
`x^2 = 4py` We can see that the parabola passes through the point `(6, 2)` Substituting, we have `(6)^2 = 4p(2)` So `p = 36/8 = 45` So we need to place the receiver 45 metres from the vertex, along the axis of symmetry of the parabola The equation of the parabola is `x^2 = 18y ` That is `y = x^2 /18`Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experienceQuestion I do not know how to graph the parabola y= x^2 Found 2 solutions by stanbon, jim_thompson5910 Answer by stanbon(757) (Show Source) You can put this solution on YOUR website!




A Quadratic Function Models The Graph Of A Parabola The Quadratic Functions Y X2 And Y X2 2 Are Brainly Com
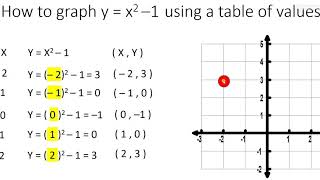



Graph Y X 2 1 Parabola Using A Table Of Values Video 3 Youtube
The graph of the straight line is above that of the parabola At any point x between 1 and 2, the vertical distance is x2x^2 So we have to find the maximum value of this function Rewrite as 2(x^2x)=9/4 (x1/2)^2 Largest value is 2,25 23K views Answer requested by David NiehausThe area bounded by the parabola `y^(2)=8x,` the xaxis and the latusrectum, is asked 2 days ago in Definite Integrals by Somyek (102k points) class12;4y 2 12x y 67 = 0;



Y X 2 2



1
The parabola defined by y = x 2 2 x − 3 has y intercept at ( 0, − 3) Where − 3 is the only term without an x in the parabola 's equation This can be seen on this parabola's graph We can see that y = x 2 2 x − 3 cuts the y axis at the point ( 0, − 3)How to Graph a Parabola of the Form {eq}Y = (xh)^2 K {/eq} Step 1 Find the vertex Since the equation is in vertex form, the vertex will be at the point (h, k) Step 2 Find the yintercept0 votes 1 answer Find the area included between the line `y=x` and the parabola `x^2=4y`



Quadratics Graphing Parabolas Sparknotes



Instructional Unit The Parabola Day 4 And 5
X2 = 4ay Standard equation of a parabola that opens up and symmetric about yaxis with at vertex (h, k) (x h)2 = 4a (y k) Graph of x2 = 4ay Axis of symmetry yaxis Equation of axis x = 0 Vertex V (0, 0) Focus F (0, a) Equation of latus rectum y = a (2, 4) The easiest way is y=ax^2bx c axis on symmetry is aos = (b)/(2a) Vertex is (aos, f(aos)) c = yintercept so your function y = x^2 4x a = 1 b = 4 c = 0 aos = ((4))/(2*1) = 2 f(aos) means we put the aos back in your function as x and solve for y f(aos) = f(2) = 2^2 4*2 = 4 Vertex is (aos, f(aos)) Vertex is (2, 4) Note, this can also be solved by completing theWe're going to explore the equation of a parabola y=a x 2 b xc for different values of a, b, and c First, let's look at the graph of a basic parabola y=x 2, where a =1, b =0, and c =0 Notice the graph opens up, the vertex is at x=0, and the yintercept is at y=0 Let's vary the value of a to determine how the graph changes



Solution How To Graph A Parabola Using Y X2 2x 8



Quadratics Graphing Parabolas Sparknotes
Ex 81, 9 Find the area of the region bounded by the parabola = 2 and = We know = & ,Given equation of the parabola is y 2 = 12x Comparing with the standard form y 2 = 4ax, 4a = 12 a = 3 The coefficient of x is positive so the parabola opens to the right Also, the axis of symmetry is along the positive xaxis Therefore, Focus of the parabola is (a, 0) = (3, 0) Equation of the directrix is x = a, ie x = 3 or x 3 = 0This is what I have so far (I'm mostly stuck on the integration part) $${dy\over dx}=2x \Rightarrow L=\int_0^1 \sqrt{1(2x)^2}dx$$ Substit Stack Exchange Network Stack Exchange network consists of 179 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers
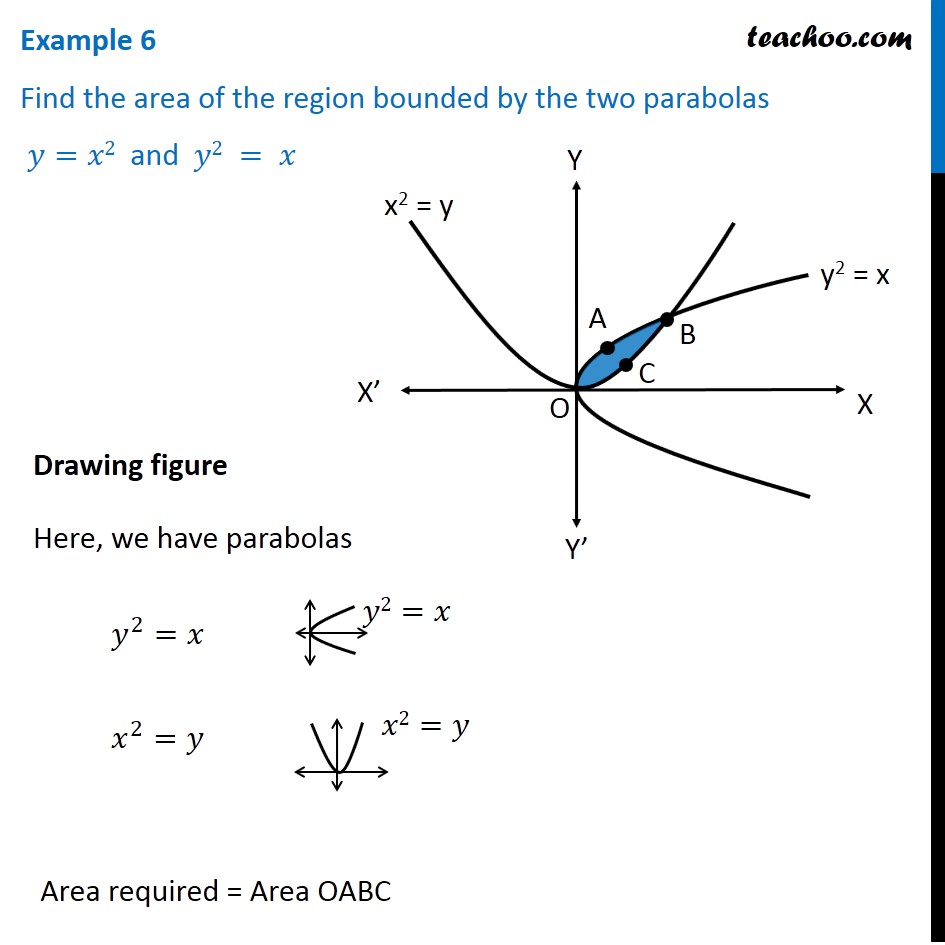



Example 6 Find Area Bounded By Two Parabolas Y X2 Y2 X




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram
Explain why or why not 97 Write the equation of a parabola that opens up or down in standard form and the equation of a parabola that opens left or right in standard form Provide a sketch of the parabola for each one, label the vertex and axis ofX 2 = 6y;This video looks at graphing the parabola 1x^2 and what happens when the coefficient is greater or less then one Lesson by Kenny Rochester, Animation by Le



Y X 2 2




How Do You Graph Quadratic Functions Y X 2 4x 7 Socratic
X 2 x 2 Set y y equal to the new right side y = x 2 y = x 2 y = x 2 y = x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = 1 a = 1 h = 0 h = 0 k = 0 k = 0 Since the value of a a is positive, the parabola opens upY = x 2 3x 13;Y = x 2 5x 3;



Misc 12 Find Area X Y Y X2 And Y X Class 12



We Know How To Graph The Quadratic Equation Y X2
Foci\3x^22x5y6=0 vertices\x=y^2 axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=x^{2} en Related Symbolab blog posts Practice, practice, practice Finding the yintercept of a parabola can be tricky Although the yintercept is hidden, it does exist Use the equation of the function to find the yintercept y = 12x 2 48x 49 The yintercept has two parts the xvalue and the yvalue Note that the xvalue is always zero So, plug in zero for x and solve for yY = a x 2 b x c In this exercise, we will be exploring parabolic graphs of the form y = a x 2 b x c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third We have split it up into three parts



Let S Begin This Investigation By Looking At Several Graphs Of Y Ax2 With Varying Values Of A For This Exploration We Will Look Specifically At A 1 5 And 5 The Graph Of A 1 Will Be Used As A Control Graph To Compare With The Graphs Of The Other Values Of A




In The Xy Plane The Parabola With Equation Y X 11 2 Intersects The Line With Equation Y 25 Youtube
Y = x 2 2x 3 ;Y = − x 2 y = x 2 y = − x 2 y = x 2 Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 1 a = 1 h = 0 h = 0 k = 0 k = 0 Since the value of a a is negative, the parabola opens down Opens Down Find the vertex ( h, k) ( h, k)Y 2 = 12x;
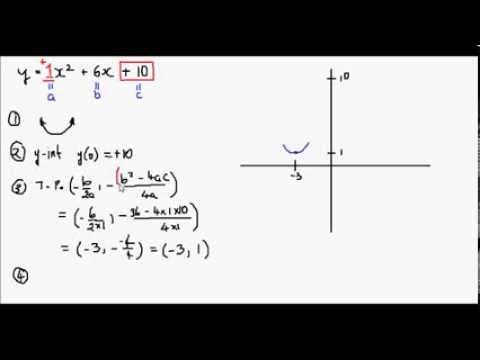



How To Sketch A Parabola Example 3 Y X 2 6x 10 Youtube
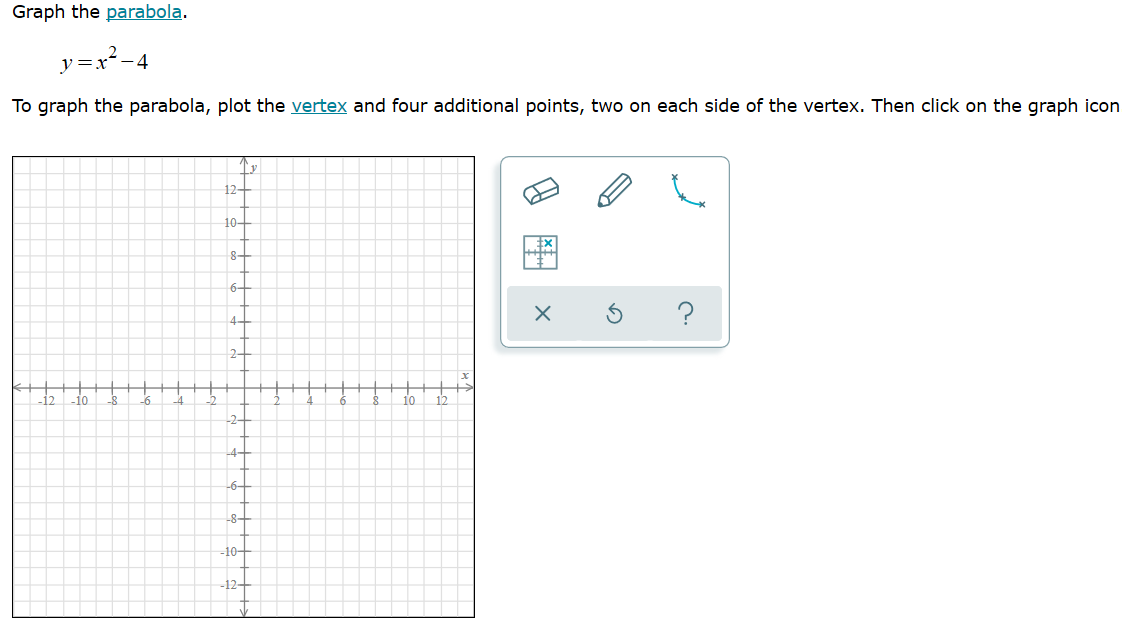



Solved Graph The Parabola Y X2 4 To Graph The Parabola Chegg Com
I do not know how to graph the parabola y= x^2 Plot a few points and draw a smooth curve thru themOn the parabola y=x 2, the point at a least distance from the straight line y=2x−4 is On the parabola yGiven, parabola is y=x 2 (i) and straight line is y=2x−4 (ii) From equations (i) and (ii), we get x 2−2x−4=0 Let f(x)=x 2−2x−4 Thus f (x)=2x−2 For least distance, put f (x)=0 ⇒2x−2=0 ⇒x=1 From equation (i), we have y=1 Hence, the point least distant from the line is (1,1) Video Explanation Solve any question of Conic Sections with




Graph Y X 2 3 Youtube




How Do You Graph Y X 2 1 Socratic
y = x 2, where x ≠ 0 Here are a few quadratic functions y = x 2 5;Graph of y = x2 The shape of this graph is a parabola Note that the parabola does not have a constant slope In fact, as x increases by 1, starting with x = 0, y increases by 1, 3, 5, 7, As x decreases by 1, starting with x = 0, y again increases by 1, 3, 5, 7, Graphing y = (x h)2 kThe general equation of a parabola is y = a (xh) 2 k or x = a (yk) 2 h, where (h,k) denotes the vertex The standard equation of a regular parabola is y 2 = 4ax Some of the important terms below are helpful to understand the features and parts of a parabola Focus The point (a, 0) is the focus of the parabola
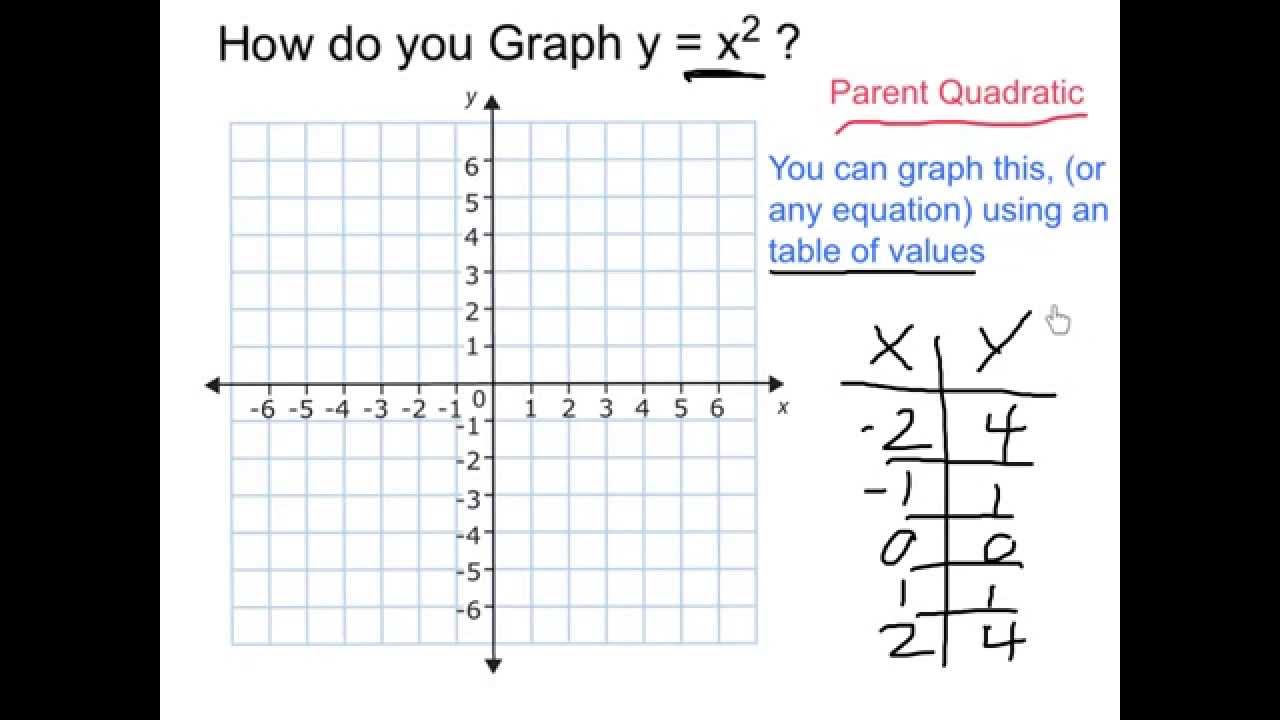



Graph Y X 2 Youtube




How To Graph A Parabola Of The Form Y X 2 Bx C Algebra Study Com
A Quadratic Equation takes the form y = ax2 bx c Graph of a quadratic function forms a Parabola The coefficient of the x2 term (a) makes the parabola wider or narrow If the coefficient of the x2, term (a) is negative then the parabola opens down The term Vertex is used to identify the Turning Point of a parabola Curve y = x 2 is a parabola whose vertex is (0, 0) and is symmetric about yaxis Equation y = x represents two lines When x > 0, then y = x When x < 0, then y = x Intersection points of y = x and parabola y = x 2 are O(0, 0) and A (1, 1) Intersection points of y = – x and parabola y = x 2 and O(0, 0) and B ( 1, 1) The region bounded by lines y = x and y = – x and The beginning of an indepth study of graphing quadratic equations (parabolas) Includes the vocab words vertex and axis of symmetry



Solution Find The Coordinates Of The Points Of Intersection Of The Parabola Y X2 And The Line Y X 2
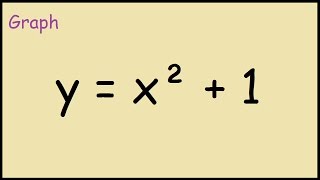



How To Graph Y X 2 1 Youtube
Practice Problems on Parabola Illustration 1 Find the vertex, axis, directrix, tangent at the vertex and the length of the latus rectum of the parabola 2 y 2 3 y − 4 x − 3 = 0 Solution The given equation can be rewritten as ( y 3 4) 2 = 2 ( x 33 32) which is of the form Y 2 = 4 a X whereDownload scientific diagram Graph of y = x 2 , the equation for a parabola from publication Quantum Gravity and Phenomenological Philosophy The central thesis of this paper is that The standard equation for a vertical parabola (like the one in the chart above) is y = x 2 For a horizontal parabola (an opening facing the left or right) the formula is y 2 = x To find the focus of a parabola, use the following formula y 2 = 4ax Example Find the focus of the equation y 2 = 5x First convert y 2 = 5x into y 2 = 4ax form



How To Plot The Graph Of The Following Y X 1 2 Quora




Quadratic Function
Answer (1 of 4) Y=05x^2, y=2/3x^2 y=ax^2 is wider than y=x^2 if a is any real number greater than 0 but less than 1 if a is greater than 1 then it will be narrowed Let's take a look at the first form of the parabola f (x) = a(x −h)2 k f ( x) = a ( x − h) 2 k There are two pieces of information about the parabola that we can instantly get from this function First, if a a is positive then the parabola will open up and if a a is negative then the parabola will open downTo find the vertex, focus, axis, directrix, latus rectum of parabolas reducible to one of the four standard forms Example 4 Find the vertex, axis, focus, directrix and latus rectum of the following parabolas y 2 8y x 19 = 0;
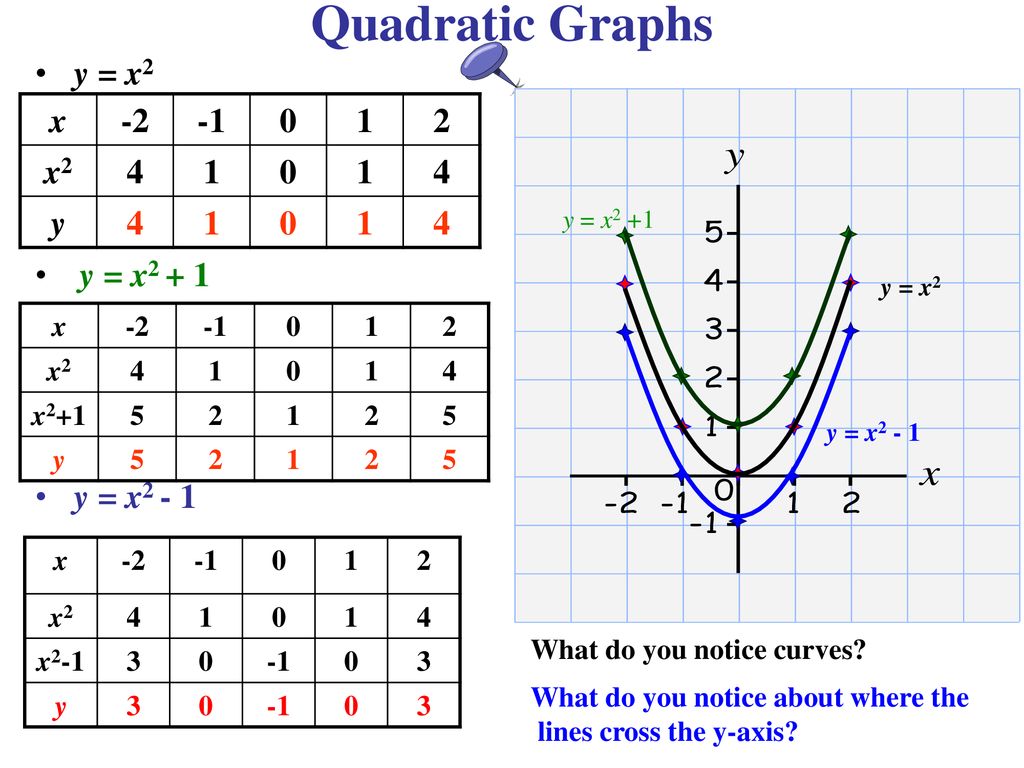



Quadratic Graphs Parabolas Ppt Download
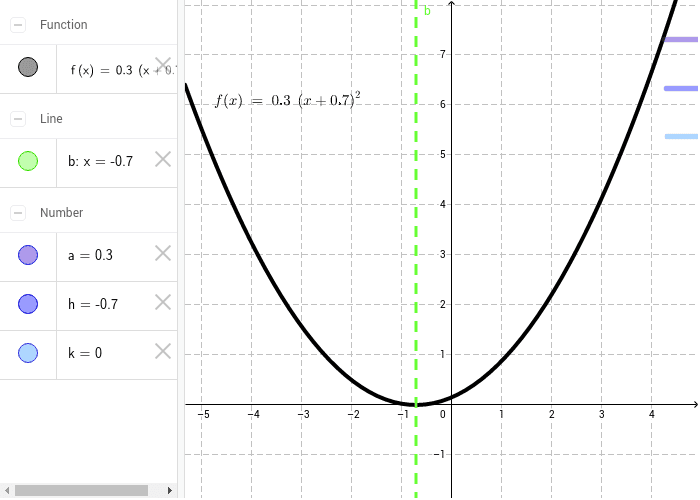



Transformations To The Graph Of Y X 2 Geogebra
And y = −√ x (the bottom half of the parabola) Here is the curve y 2 = x It passes through (0, 0) and also (4,2) and (4,−2) Notice that we get 2 values of y for each value of x larger than 0The equation of a parabola graph is y = x² Parabolas exist in everyday situations, such as the path of an object in the air, headlight shapes and the wire of suspension bridges I was studying line integral for some pdfs and came up with the following question ∫ γ ( x − 2 y 2) d y, γ is the arc of the parabola y = x 2 from ( − 2, 4) to ( 1, 1) I used the parameterization γ ( t) = ( t, t 2) , γ ′ ( t) = ( 1, 2 t) e ‖ γ ′ ( t) ‖ = 1 4 t 2, but when i do ∫ − 2 1 ( t − 2 t 4) 1 4 t 2 d t It does not work
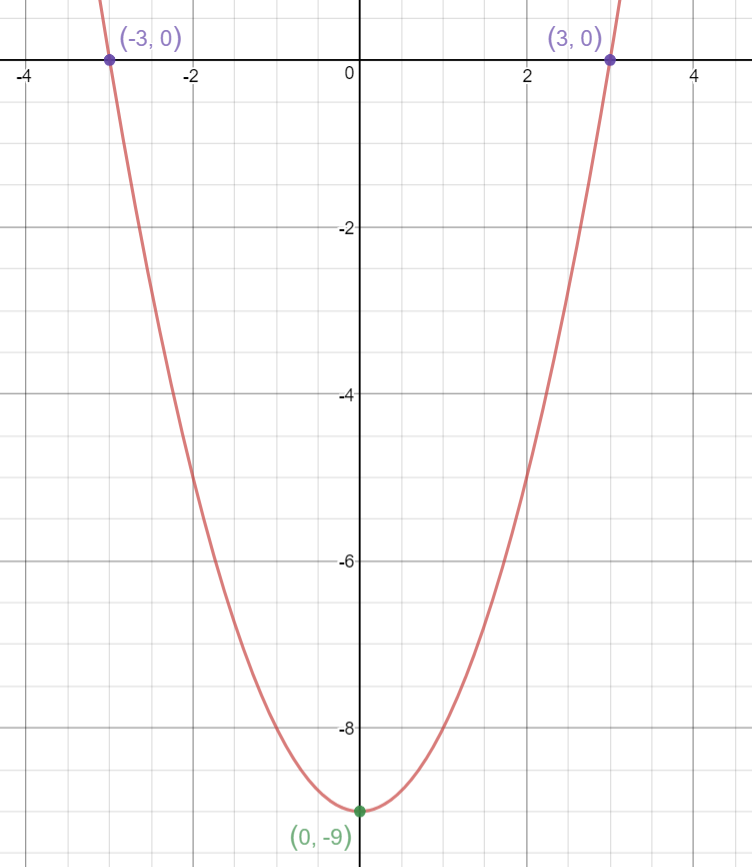



How Do You Graph Y X 2 9 Socratic



Solution Graph Y X 2 1 Label The Vertex And The Axis Of Symmetry And Tell Whether The Parabola Opens Upward Or Downward
The children are transformations of the parent Some functions will shift upward or downward, open wider or more narrow, boldly rotate 180 degrees, or a combination of the above Learn why a parabola opens wider, opens more narrow, or Column A A1 Make it X place a negative number, like 10 or100 A3 next number in sequence, like 9 or 99 select the two numbers, and drag down until your at 10 or 100 B Make it Y B2 put in formula, =A^23 Drag downIs the parabola x = y 2 x = y 2 a function?




Consider A Parabola P That Is Congruent To Y X 2 Opens Upward And Has Vertex 0 0 Find The Brainly Com



Y X 2 2
PARABOLAS TRANSLATIONS AND APPLICATIONS QUADRATIC RELATION A quadratic relation in two variables is a relation that can be written in the form y=ax^2bxc or x=ay^2byc where a, b, and c are real numbers, and a!=0 The graphs of quadratic relations are called parabolas The simplest quadratic relation of the form y=ax^2bxc is y=x^2, with a=1, b=0, and c=0, so this



Graphing Quadratic Functions
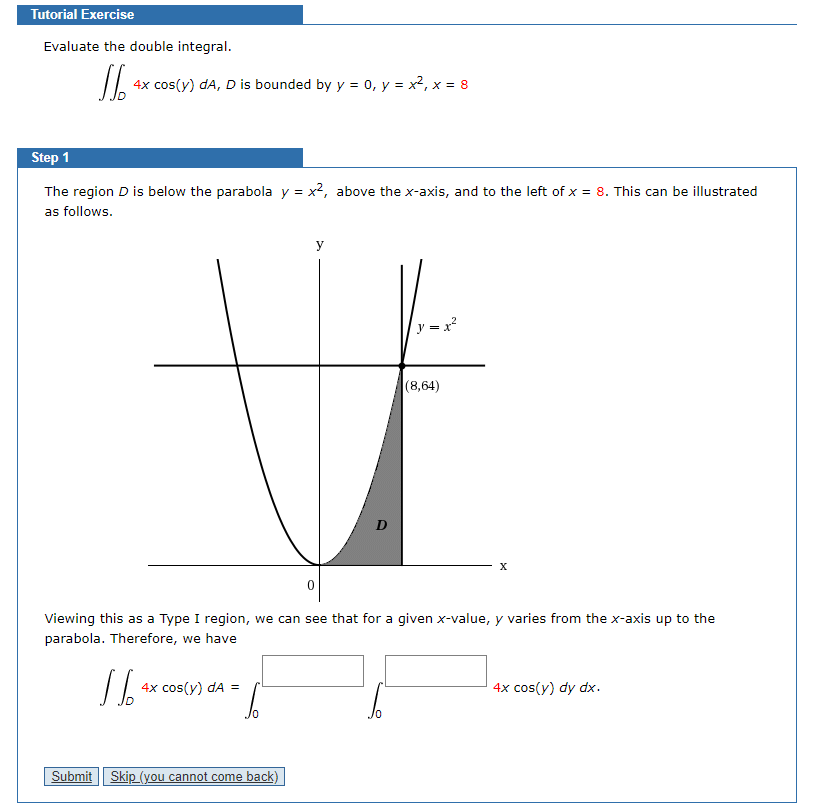



Solved Tutorial Exercise Evaluate The Double Integral 4x Chegg Com
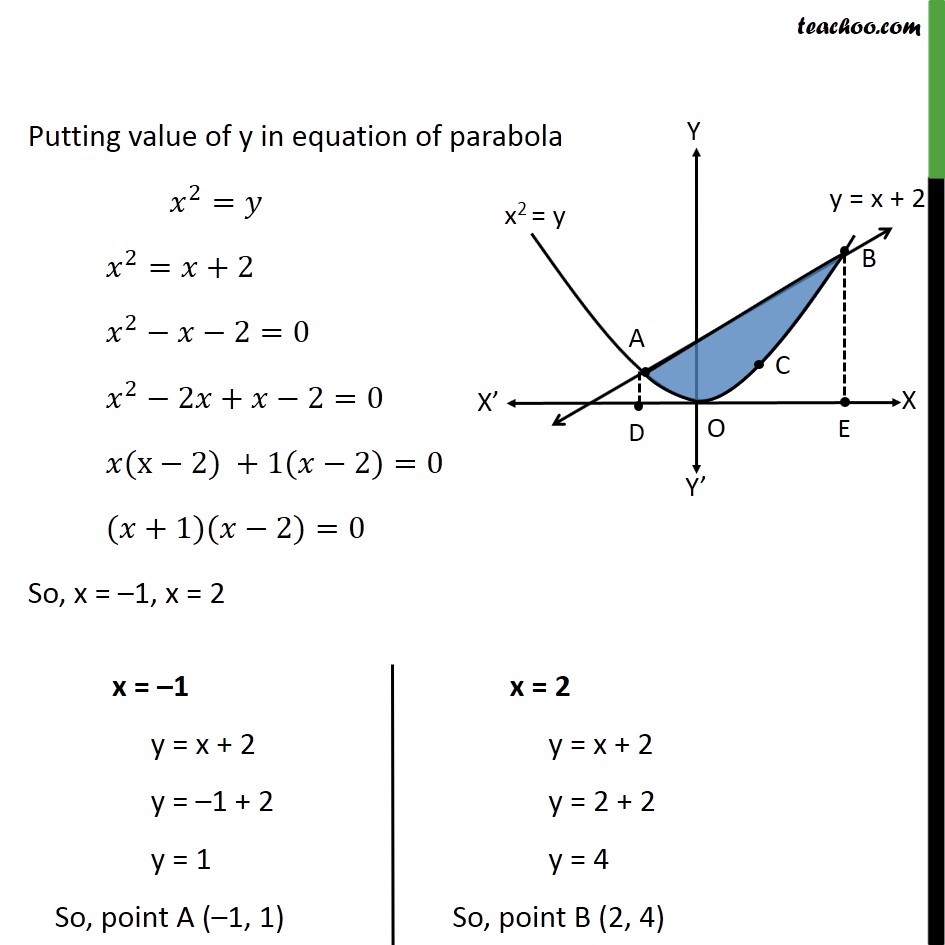



Misc 10 Find Area Enclosed By Parabola X2 Y T X 2



Quadratics Graphing Parabolas Sparknotes




Solution For The Parabola Y X 2 36 Graph Of A Parabola Opening Down At The Vertex 0 36 Crossing The X Axis At 6 0 And 6 0



Parabola Y X 2 Geogebra



Graph The Parabola Y X 2 6x Mathskey Com
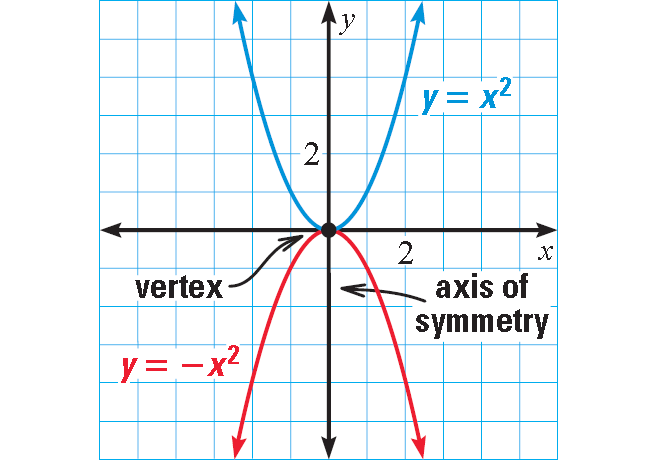



Graphing Quadratic Functions Parabola



How Do You Sketch The Graph Of Y X 2 2x And Describe The Transformation Socratic



Exploration Of Parabolas




The Line Y X 2 Cuts The Parabola Y 2 8x In The Points A And B The Normals Drawn To Youtube



Solution I Do Not Know How To Graph The Parabola Y X 2



Quadratics Graphing Parabolas Sparknotes



Solution How Do You Graph Y X 3 2 2
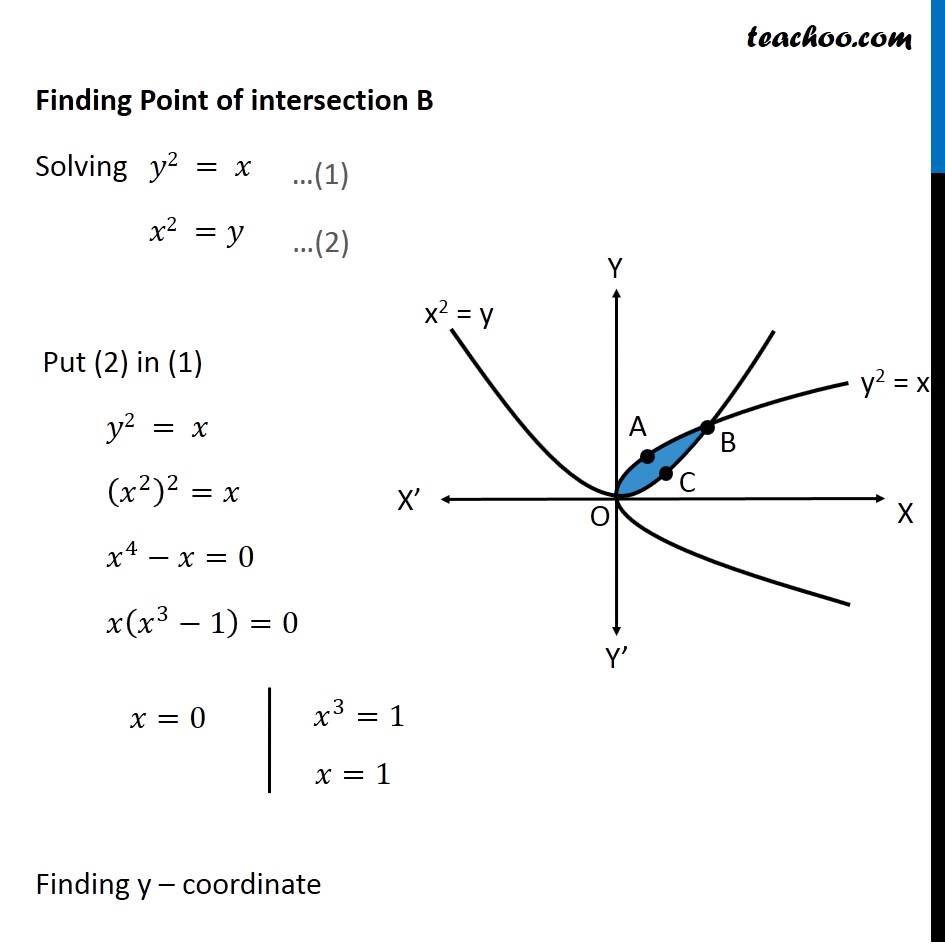



Example 6 Find Area Bounded By Two Parabolas Y X2 Y2 X




Transformations Of Quadratic Functions College Algebra
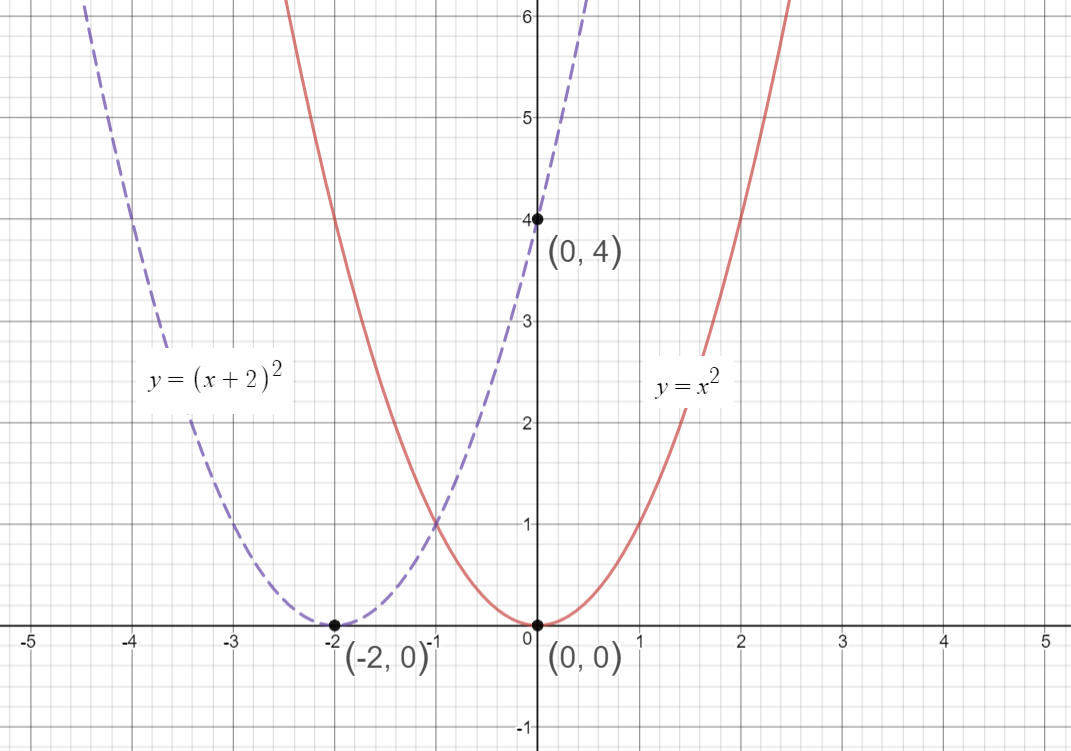



How Do You Sketch The Graph Of Y X 2 2 And Describe The Transformation Socratic



Y X 2




Draw The Graph Of Y X 2 And Y X 2 And Hence Solve The Equation X 2 X 2 0




Quadratic Function



Instructional Unit The Parabola Day 4 And 5




How To Draw Y 2 X 2 Interactive Mathematics



Exploration Of Parabolas



How Do You Sketch The Graph Of Y X 2 8 And Describe The Transformation Socratic
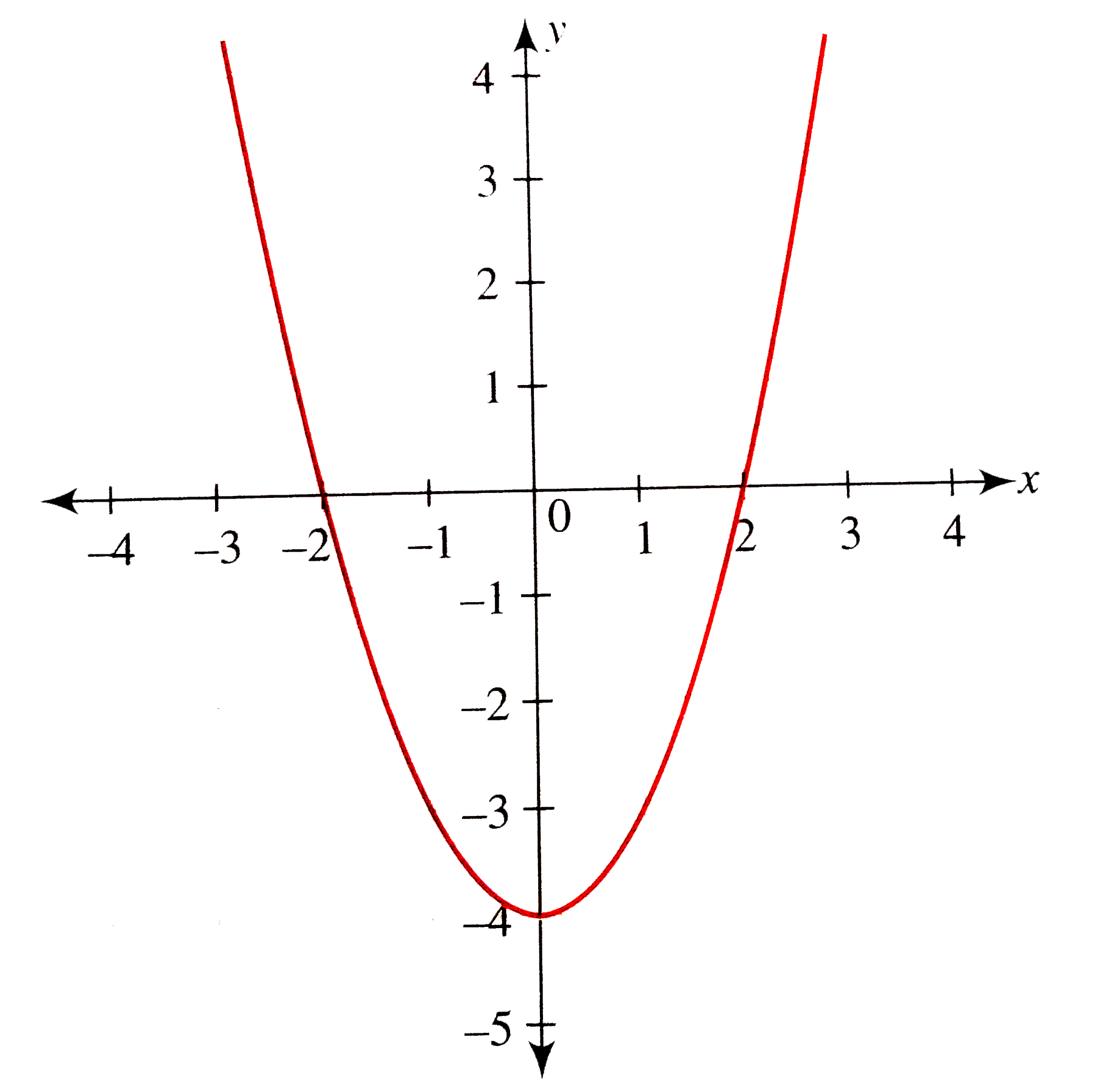



From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4
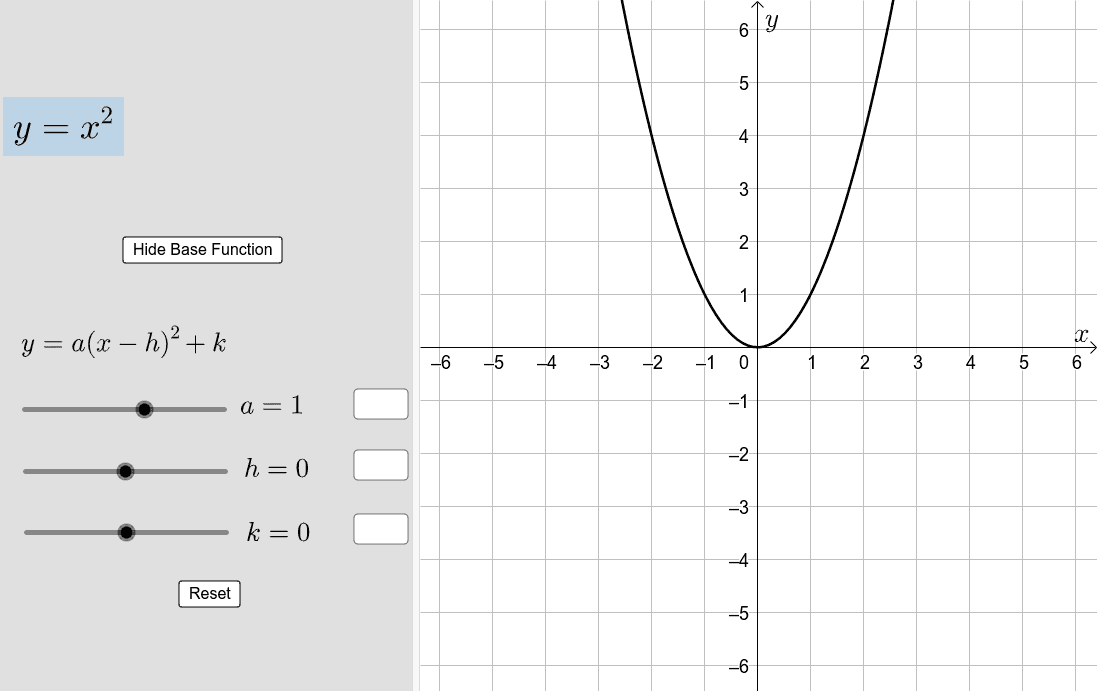



Transforming The Graph Of Y X Geogebra
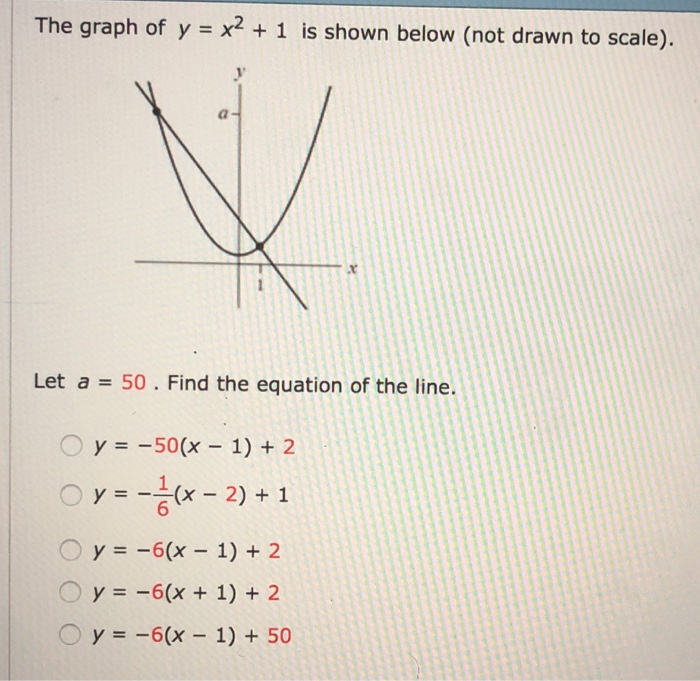



Solved The Graph Of Y X2 1 Is Shown Below Not Drawn To Chegg Com



Sketch The Parabola Of Equation Y X 2 6x 9 And Indicate Its Vertex Study Com




Draw The Graph Of Y X 2 X 2 And Find Its Roots



Untitled Document
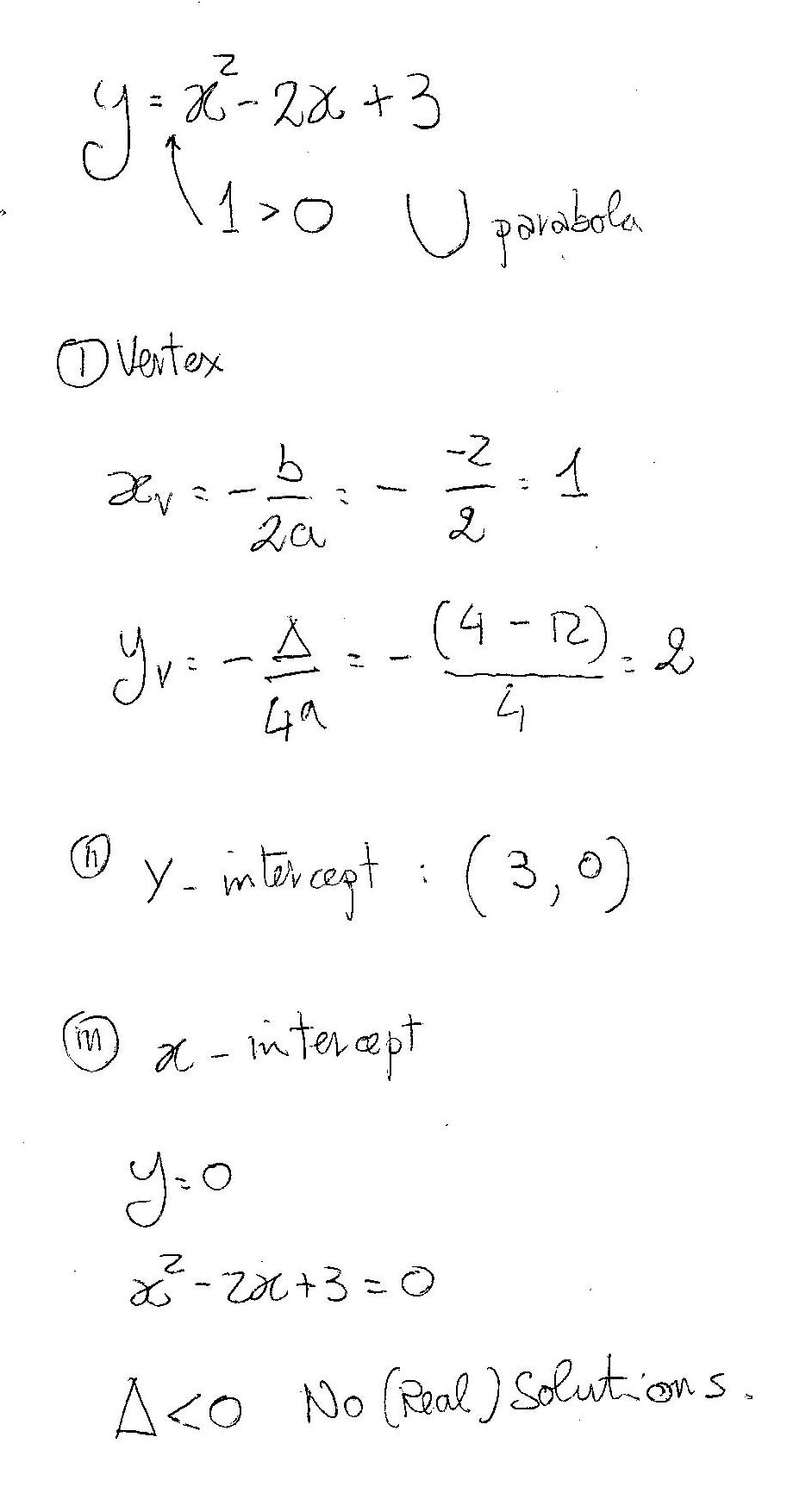



How Do You Graph Y X 2 2x 3 Socratic
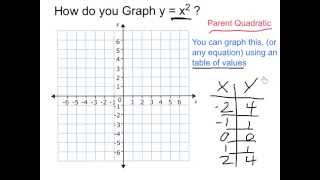



Graph Y X 2 Youtube




How To Graph Y X 2 1 Youtube




Graph Showing The Translation Of Y X 3 2 Download Scientific Diagram




Consider The Parabola Y X 2 The Shaded Area Is Brainly In
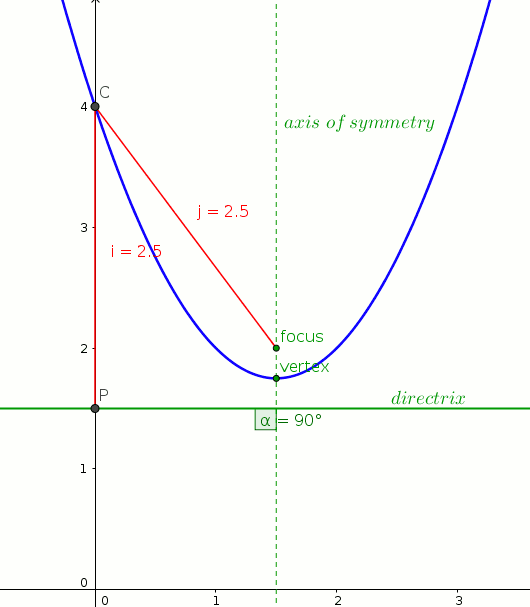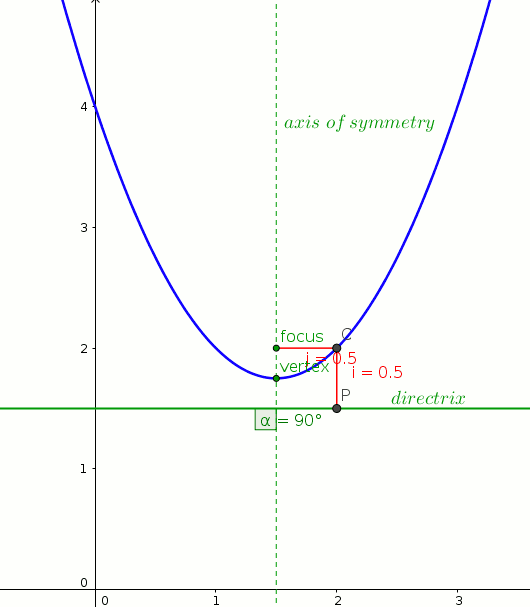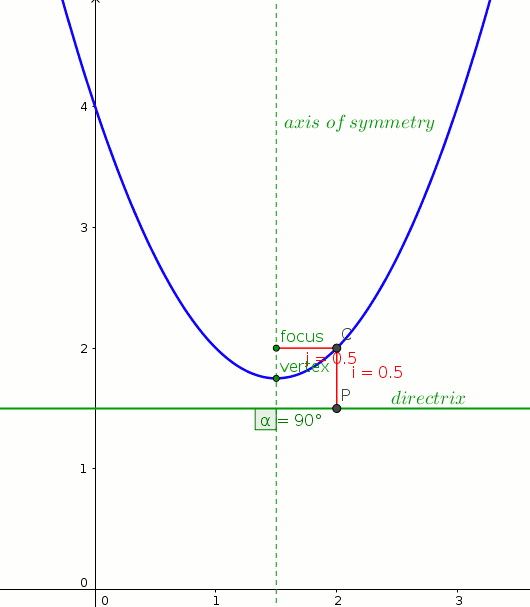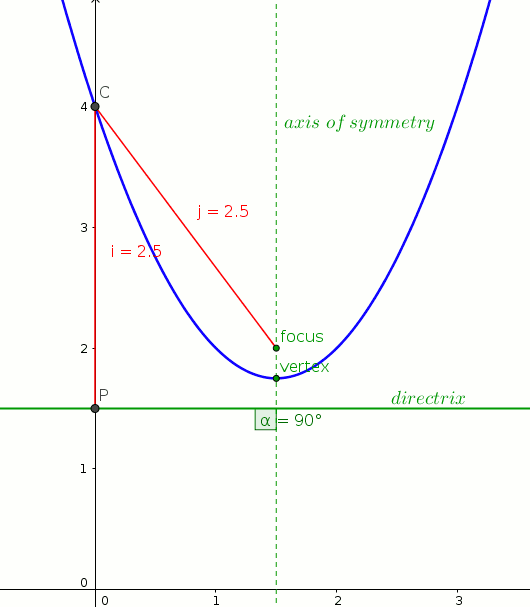



What Are The Vertex Focus And Directrix Of Y X 2 3x 4 Socratic
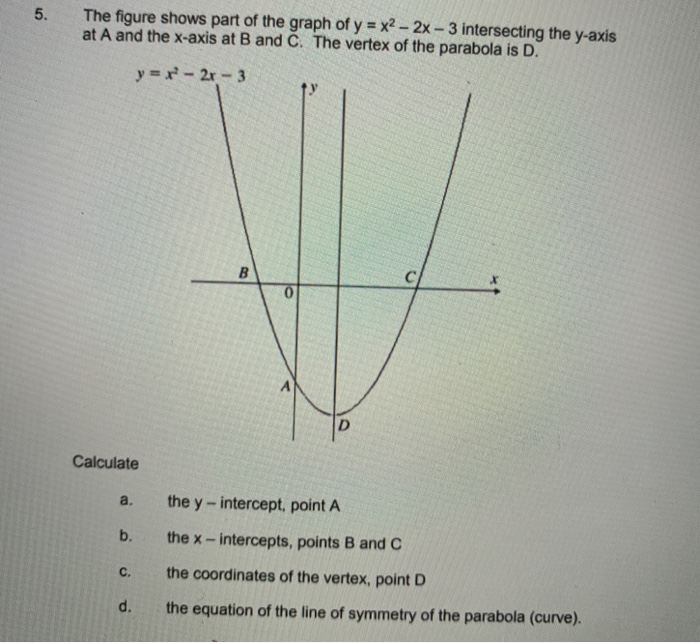



Solved 5 The Figure Shows Part Of The Graph Of Y X2 2x Chegg Com
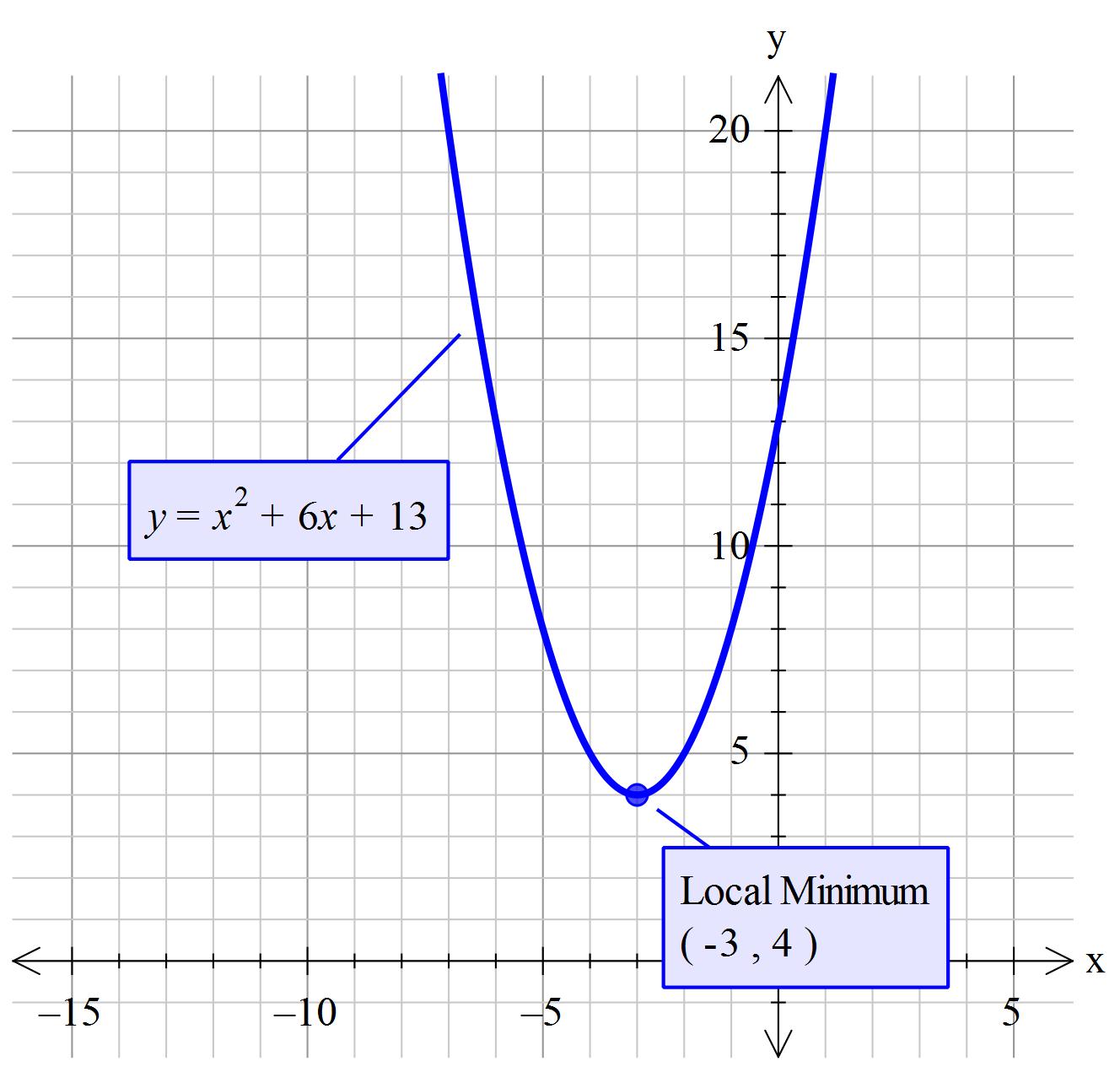



What Is The Axis Of Symmetry And Vertex For The Graph Y X 2 6x 13 Socratic
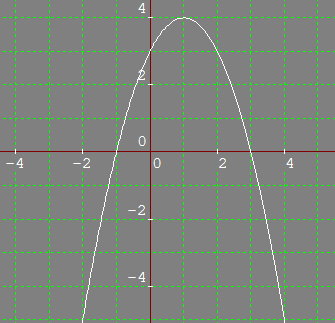



How Do You Graph Y X 2 2x 3 Socratic
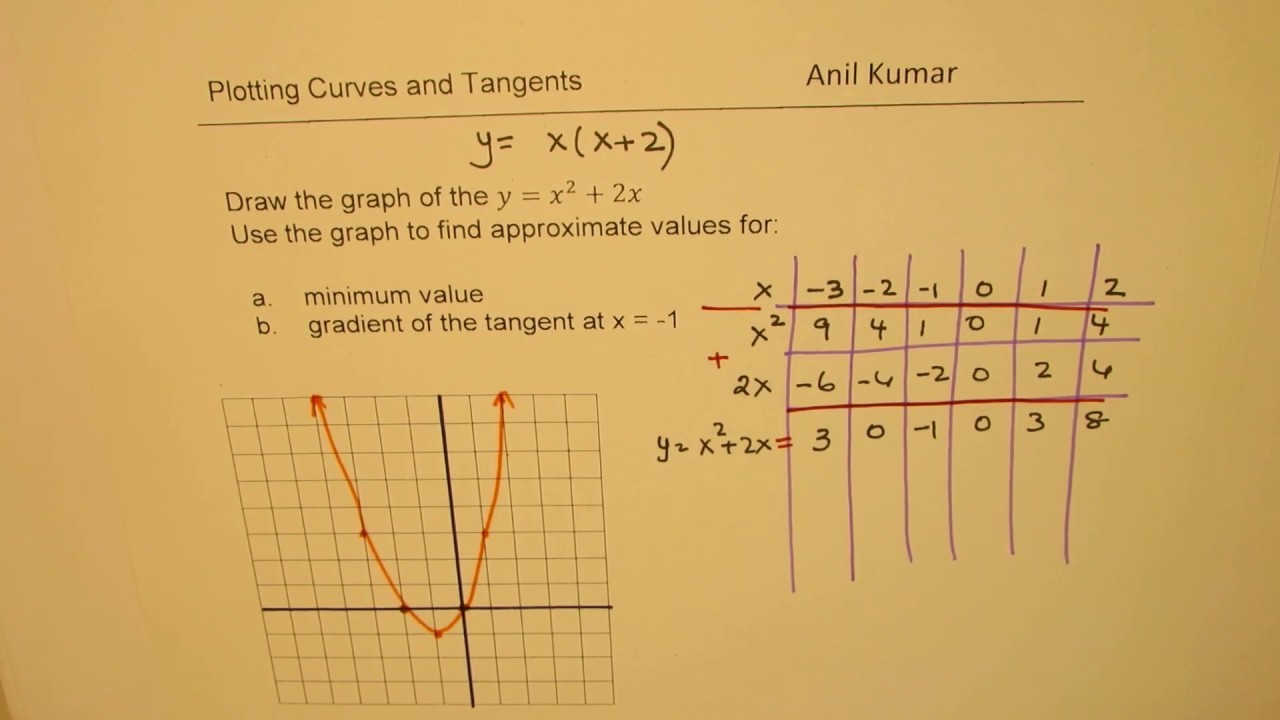



Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube




Find The Area Of The Region Bounded By The Parabola Y X 2 And The Line Y 4 Study Com




How To Graph A Parabola Y X 5 2 3 Socratic



Practice Exam 1




Graph The Parabola Y X 2 Be Sure To Label Any Important Quizlet



1




Draw The Graph Of Y X 2 And Y X 2 And Hence Solve The Equation X 2 X 2 0
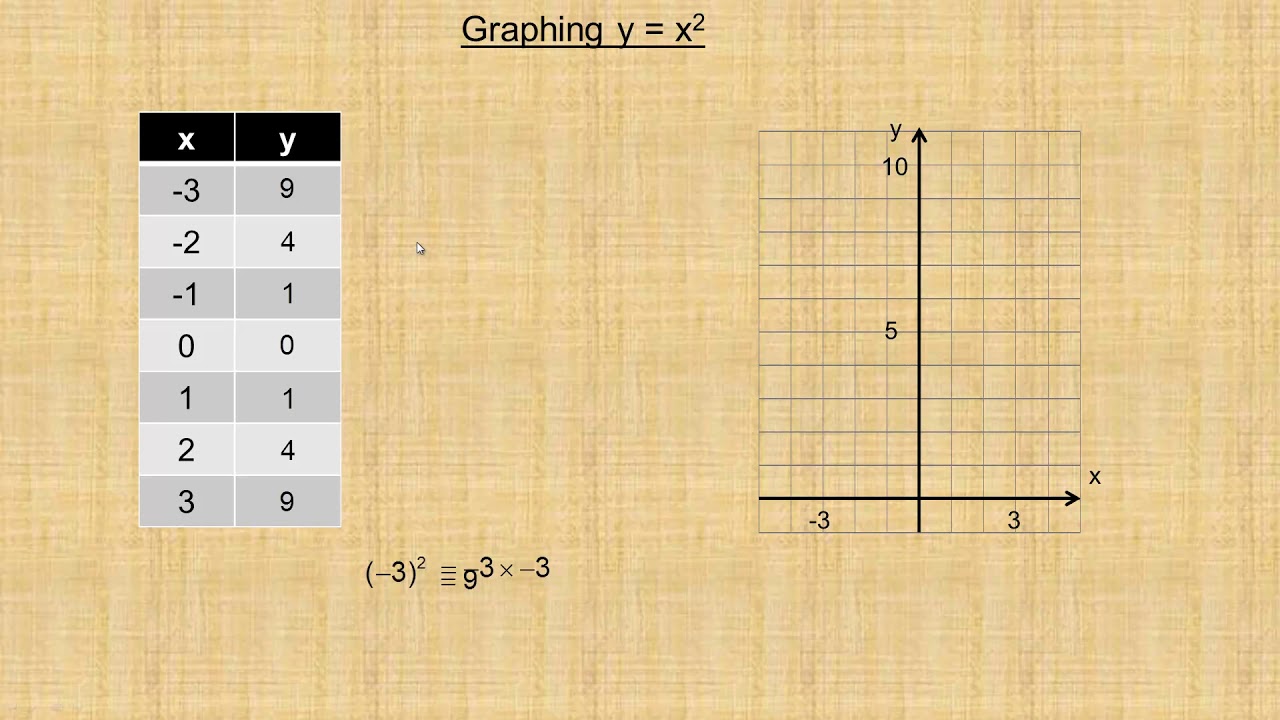



Graphing Y X Youtube



Instructional Unit The Parabola Day 4 And 5




Find The Coordinates Of A Point Of A Parabola Y X 2 7x 2 Which Is Closest To The Straig Youtube



1
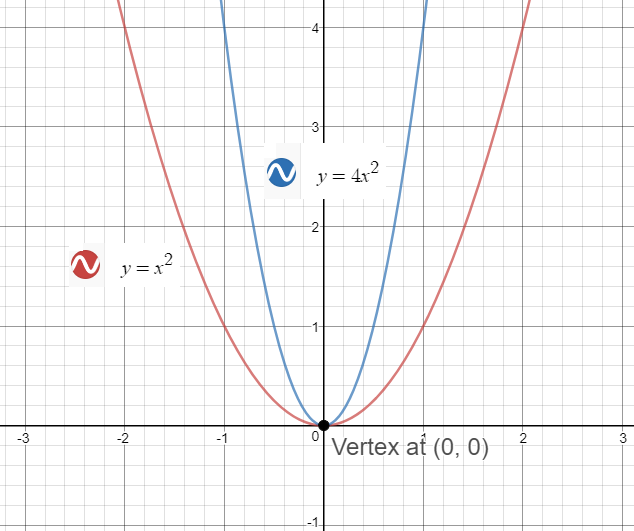



How To Graph A Parabola Y 4x 2 Socratic




Graph Y X 2 Study Com



Solution How Do You Graph Y X2 6x 8
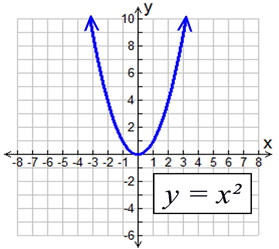



Parabola Parent Function Mathbitsnotebook A1 Ccss Math




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram




Content Transformations Of The Parabola



Graphing Quadratic Functions



How Do I Graph The Quadratic Equation Y X 2 4x 6 Socratic




How Do You Graph Y X 2 2x Socratic
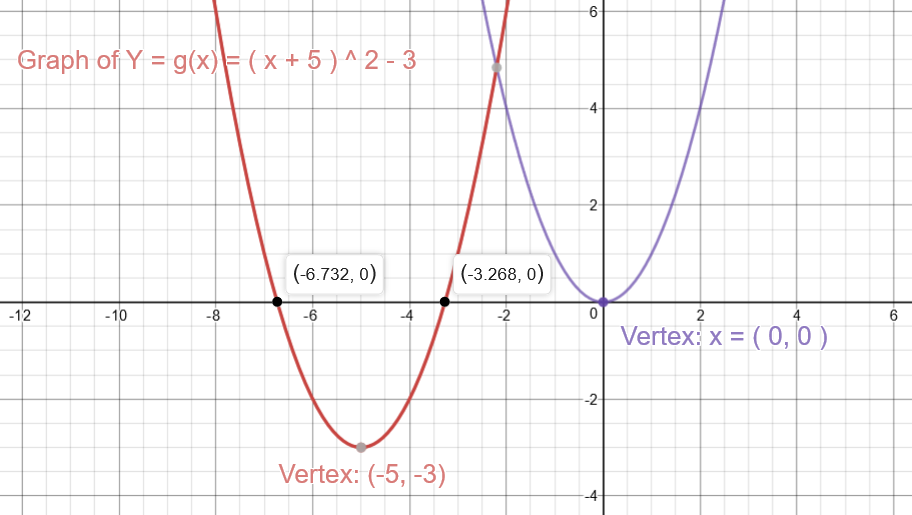



How To Graph A Parabola Y X 5 2 3 Socratic



What Is The Vertex Of Y X 2 6 Socratic




Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic



Quadratics Graphing Parabolas Sparknotes
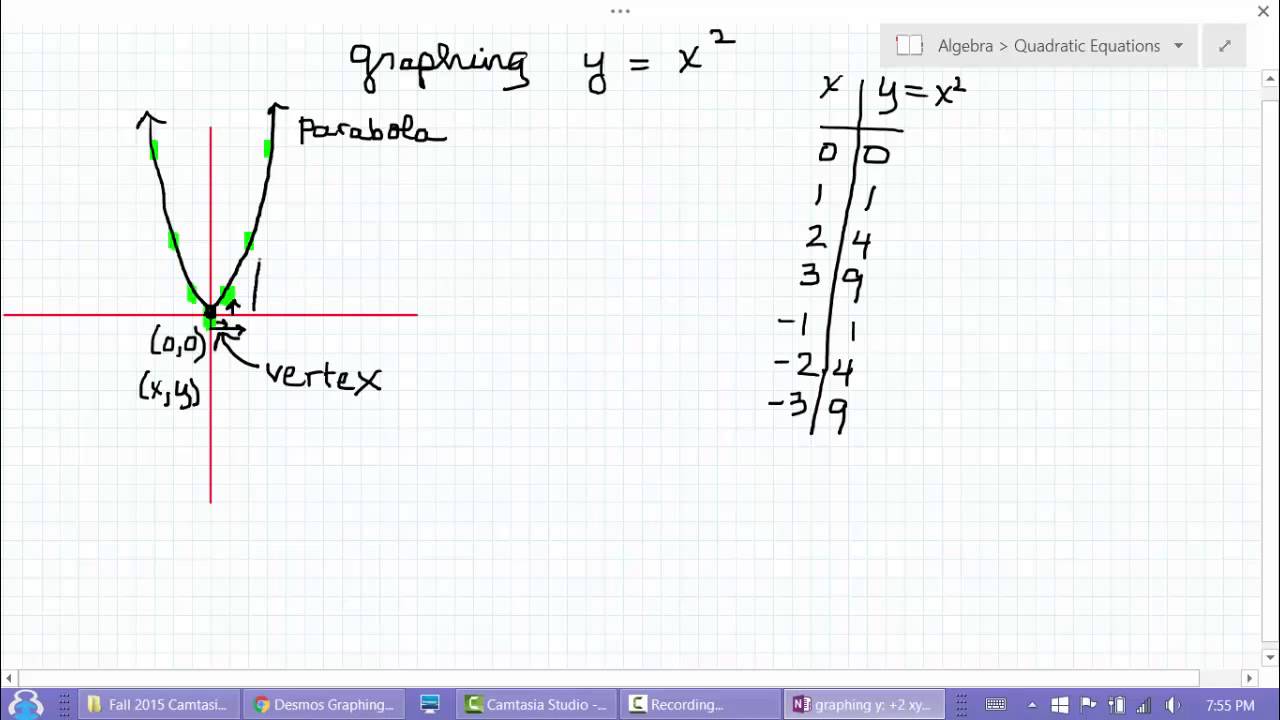



Graphing Basic Parabola Y X 2 Youtube




Content Transformations Of The Parabola




Y X 2 16x 28 The Equation Above Represents The Graph Of A Parabola In The Xy Plane Which Of The Following Represents An Equivalent Form Of The Equation That Includes The Minimum Value Of Y As



Solved 1 Compare The Graph Of Y X 2 To The Graph Of Y 0 6 X 2 A Which Course Hero
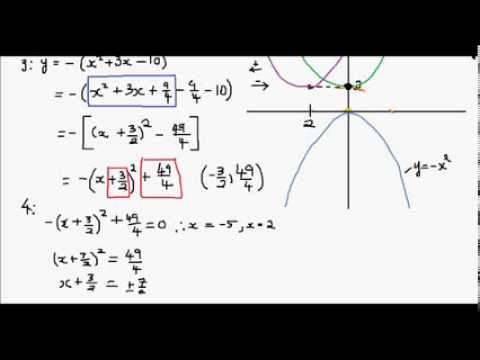



How To Sketch A Parabola Example 1 Y X 2 3x 5 Youtube




How To Graph A Parabola Of The Form Y A X H 2 K Algebra Study Com



Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively




Parabola Parent Function Mathbitsnotebook A1 Ccss Math




Graph Y X 2 1 Parabola Using A Table Of Values Video 3 Youtube
コメント
コメントを投稿