合同 式 解き方 259339-合同�� 解き方 x二乗
今まで 合同式の定義を扱った記事 フェルマーの小定理を証明した記事 倍数の判定法について解説した記事(前編と後編)といったように、「合同式」にまつわる記事を書いてきました。 我々が解きたい問題たち 問題を解くときの考え方 中国剰余 解き方が別の合同式だと思うのですが、それぞれの問題の解き方を教えてください。 一つ目 次の合同式を解く、または、解けないことを証明せよ。 (a) 3x^2 5x 7 ≡ 0 (mod 1312 2次合同式 ax2 bxc 0 mod p は解けるか? 13 演習 (1) x2 x 1 0 mod p を,p = 2;3;5;7;11 のときに解け(解がないことがあ りうる). (2) x2 x 2 0 mod p を解け. 14 解の導き方 複素数体上では,係数で割る(係数のかけ算に関する逆元をかける)という操作を

ユークリッドの互除法は無理という人へ 不定方程式は合同式を試してみて 数学のコツ壺 風いま数学協室
合同式 解き方 x二乗
合同式 解き方 x二乗-合同式modの使い方(問題編) 例題:2^50を5で割った時の余りを求めよ。 (解法案11)規則性を見つける。 (解法12)合同式を利用する;合同式を用いると、問題は、次のように書き直すことができる。(合同式→こちらを参照) 同時に満たす X を求めよ。 これは、正しく連立合同式の問題である。この連立合同式の解法については、Gauss の方 法が知られている。




整数 1次不定方程式 合同式 Mod 利用 裏技 数学メモランダム
合同式に慣れていない場合は、この方法がおすすめです! おすすめ2 合同式を使う方法 一番スマートな方法です。 合同式の式変形に慣れている場合は、この方法がおすすめです! 特殊解だけでなく、直接整数解を求めることが可能なのでとても便利です。代数入門演習 NO 9 13 123 9 1次合同式, 連立1次合同式(中国の剰余定理), Euler関数 第911 節では, 参考のために1 次合同式の一般的解法(定理91) を解説する 第912 節で は, 有限集合の写像に関する重要な性質(命題93)の証明を念のために書く 91 解説編 911 1次合同式の一般的解法, 連立1次合同式 二次方程式は「①解の公式②因数分解③√」による解き方で解きます。 本記事では「二次方程式とは何か」という説明から、3つの解き方の使い分けまでを解説します。 もし、上の3つの二次方程式の解き方を使 55 akk
合同式による整数方程式の解法 合同式は、整数の余りの計算法としてガウスによって考えられました。合同式を使うことによって、割合簡単に整数解を求めることができます。使いこなせるようにしておいて損はないと思います。 合同式の定義・性質 1合同式 11と18を7で割ると、どちらも余りが4になりますが、これを記号「≡」を用いて合同式というもので表す と、11 となり、『11と18は を法として合同である』と言います。簡単に言えば、「11と18は で割った余りが同じ」ということです。 ≡18 (mod 7) 7 7 一般的には、n (≧2)で割ったとき、余り合同式の方程式の解法 を解くとき,両辺を3でわって,χ=2 とする。 この「3でわる」という操作は,3の逆数である1/3 をかけるという操作と同じである。 乗法に関する実数の単位元は,1 であり,ab=1 のとき,aとbは逆数の関係にある. となる.
合同式 a a , b b を整数, m m を自然数とする. a a を m m で割ったときの余りが b b のとき, ( a a や b b は m m より大きくても小さくてもいいし,負の数でも構わない.) a ≡ b ( mod m) a ≡ b ( mod m) と表す. ※ a a 合同 b b モッド m m , m m を法として a a と b b22年4月17日 このページでは、 数学A「合同式」の問題と解答をまとめています。 合同式の計算、合同式と余り、合同式と証明 など、合同式の問題一覧にしてあります。 目次 1 合同式 問題と解答一覧 2 合同式の解説 1A = 1 のときでも,すでにいろい ろな場合があることを確かめよう. 14 演習 (1) x2 x 1 0 mod p を,p = 2;3;5;7;11 のときに解け(解がないことがあ りうる). (2) x2 x 2 0 mod p を解け. 15 解の導き方




合同式を使って不定方程式を解く方法 W 錬成会学習塾




整数問題の難問 良問3選 解き方のコツやおすすめ参考書を解説します 遊ぶ数学
解き方が別の合同式だと思うのですが、それぞれの問題の解き方を教えてください。 一つ目 次の合同式を解く、または、解けないことを証明せよ。 (a) 3x^2 5x 7 ≡ 0 (mod 13) (b) 5x^2 6x 2 ≡ 0 (mod 13) (c) x^2 7x 10 ≡ 0 (mod 11) 二つ目 29の原始根は2であり、指数 合同式の定義 整数a,b 自然数nに対して a ≡ b (mod n) a ≡ b ( mod n) aをnで割ったあまり と bをnで割ったあまり が等しいことを表し、 「aとbはnを法として合同である」という 例えば、 10と4は3で割った時の余りが「1」で等しいので 10 ≡ 4 (mod 3) 10 ≡ 4 ( mod 3 合同式とはなにか 整数問題の中でも特によく出題されるのが剰余に関わる問題です.剰余とは余りのことで,たとえば,『$2^{40}$ を $7$ で割った余りを求めよ.』などのように余りを問う問題がよくあります.また,不定方程式の整数解を求める際にも,剰余の考え方を用いるこ




合同式 素数じゃない数のmod 2次の合同式の解き方 Youtube




高校数学a 合同式 Mod 問題一覧 合同式の計算 余り 学校よりわかりやすいサイト
応用合同式の最後で見た内容とほぼ同じです。$17$ を法としたときに、 $1$ や $1$ と合同となるような $2^k$ を探すようにします。 計算していくと、しばらく見つかりませんが、頑張って続けると\ 2^8=256=17\times151 \にたどりつけます。 今回は連立一次合同方程式の解についてです スポンサーリンク // 連立一次合同方程式を解く 〆 連立一次合同方程式を解く 次の連立合同方程式を解くとします ここで とします (1)より, は任意の整数 を用いて と表せます これは (2) を満たすので となります, つまり は の倍数なので, 任意の 合同式(mod)を使うメリット 表記簡略化による本質的な嬉しさ 「 12 12 12 と 7 7 7 を 5 5 5 で割った余りは等しい」と書くよりも 「 12 ≡ 7 (m o d 5) 12\equiv 7\pmod{5} 12 ≡ 7 (mod 5) 」と書く方が楽です。 ほとんど差がないように感じますが,記述式で複雑な問題になると上記のような文言を大量に書く必要
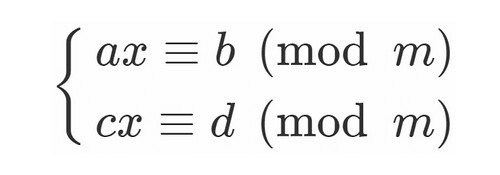



数学 連立一次合同方程式の解法 もう一人のy君




整数 1次不定方程式 合同式 Mod 利用 裏技 数学メモランダム
13 2次合同式 ax2 bxc 0 mod p は解けるか? p = 2;1 合同式(mod)とは 合同式とは、割り算の余りが等しいことを表現した式のことです。 例えば となります。 のように、一行ずつ書く方が一般的です。 そのとき、 は毎回書かなければいけません。 2 合同式の足し算・引き算・掛け算 合同式とは 2 2 つの整数 a, b a, b を m m で割った余りがどちらも r r だったとすると、 a= mpr, b =mqr a = m p r, b = m q r ( p, q p, q は整数)って表すことができるよね。 このとき a−b= m(p−q) a − b = m ( p − q) になるから a−b a − b は m m の倍数 って言えるよね




数a 合同式modと割り算の余り Youtube




整数 合同式 Mod とは 定義 性質 計算方法 数学メモランダム
少し前に合同式を使う入試問題の典型問題の解き方を解説しました。 今回は、互除法が通常用いられることの多い不定方程式を、合同式を 利用して高速に解く方法の解説をします。 例によってノートの画像から♬ 上の赤枠内の3行目、 6y≡-1≡10 ( mod 111次不定方程式 axby=1 の整数解を求める方法を4通り紹介します。 axby=1 の解き方を知っていればaxby=c も解けます。 →1次不定方程式を解くときに知っておきたい3つの基本知識 当記事では、次の例題を4通りの方法で解きます。合同方程式 の解 について 1) と が互いに素のとき,解はただ1つ存在する. 2) の最大公約数が で, が で割り切れるとき, 個の非合同解が存在する. 3) の最大公約数が で, が で割り切れないとき,解は存在しない. 例題11 を解いてください




整数問題 解法のパターン30 松田聡平 数学 Kindleストア Amazon




だいたい仕組みは分かるのですが 表で 1 の場合xを4 2 ではxを8まで Clearnote
合同式を利用した解き方では、 法に定めた数で割ったときの余り に注目して解いていきます。上手に利用できれば、式変形や面倒な計算がないので、とても有効な解き方です。 合同法を利用して不定方程式の一般解を求める手順は以下のようになります。 以下の記事で、同じ問題を合同式で解いているので確認してみてください! 合同式(mod)とは?性質の証明や計算問題の解き方 ※ ただし、合同式をしっかり理解しないで利用するのはオススメできません。




差がつく 合同式 基本編 数学の2次試験で合同式を使いこなす マスマス学ぶ




記述量を大きく削減する合同式を生徒に紹介しよう 塾講師ステーション情報局



Studydoctor 数a 合同式modと割り算の余り Studydoctor




裏技 合同式 Mod で一次不定方程式を一瞬で解く方法 Mp3




合同式 Mod とは 性質の証明や計算問題の解き方 受験辞典



写真の問題は合同式で解くことは可能てすか 可能な場合は解き方 Yahoo 知恵袋




14年11月 怜悧玲瓏 高校数学を天空から俯瞰する
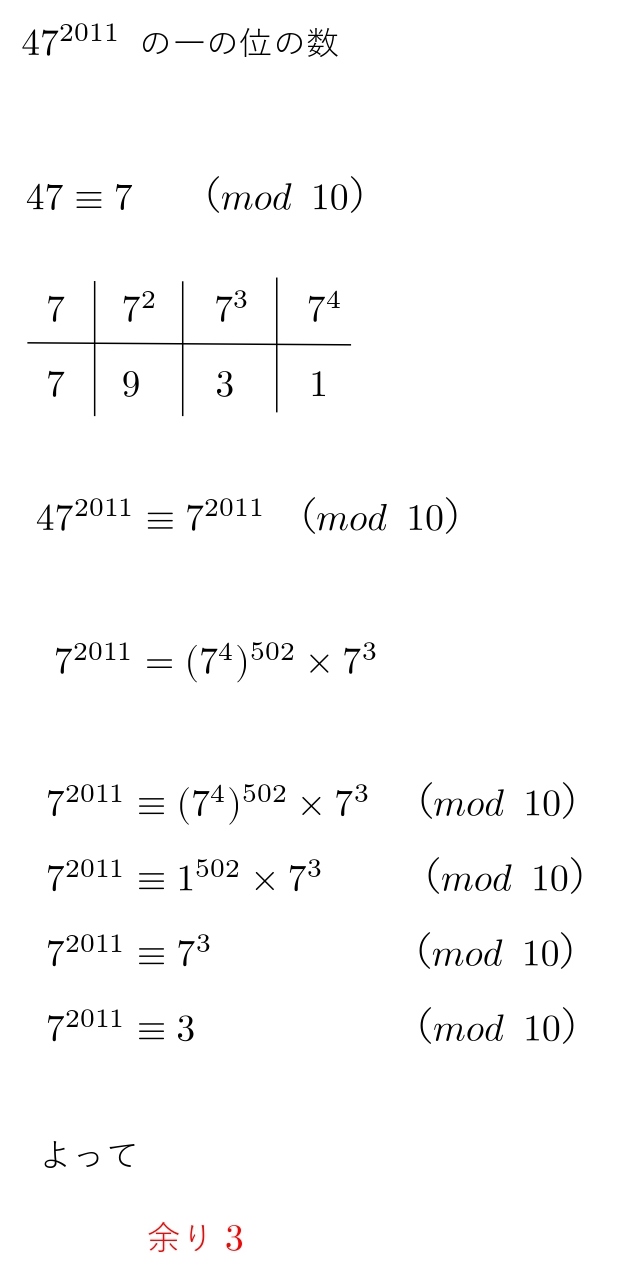



高校数学a 合同式 Mod とは 問題 解説 公式 学校よりわかりやすいサイト




22共通テスト整数 11 5x 2 5y 1 誘導なし 1次不定方程式 合同式 パスカルの三角形 マスマス学ぶ




ゆーきが教える数学ブログ




ユークリッドの互除法は無理という人へ 不定方程式は合同式を試してみて 数学のコツ壺 風いま数学協室




合同式 Mod を応用して京大入試問題を解こう 不定方程式の問題も解説 遊ぶ数学




1次不定方程式の解き方 数学a 整数 東大合格コム




合同式 Mod を応用して京大入試問題を解こう 不定方程式の問題も解説 遊ぶ数学




共通テスト前日 一次不定方程式解くのは互除法より合同式のほうが絶対楽 受験生必見 Mp3




爆速 一次不定方程式の整数解を合同式で見つける方法 ラディカル高校数学




裏技 合同式 Mod で一次不定方程式を一瞬で解く方法 Mp3




合同式の方程式の解き方 簡単バージョン 錬成会学習塾
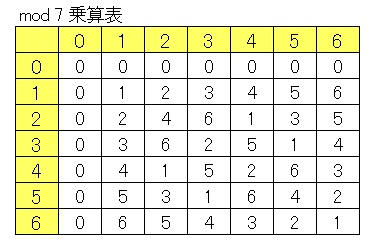



乗算表 乗法表 を用いて一次合同方程式を解く Excel Vba 数学教室
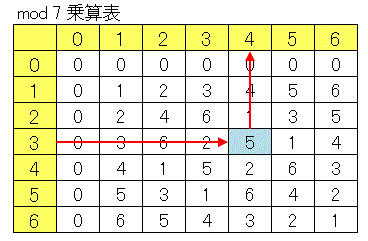



乗算表 乗法表 を用いて一次合同方程式を解く Excel Vba 数学教室



以下の合同式の解き方を教えてください 答えは最も小さい正の整数 Yahoo 知恵袋



連立合同式の問題です X 2 Mod3 X 3 Mod5 X 5 M Yahoo 知恵袋



数学a 整数の問題で合同式を使ってみよう 日々是鍛錬 ひびこれたんれん




合同式 Twitter Search Twitter



一次連立合同式の解き方を教えてください 中国剰余定理はあまりに Yahoo 知恵袋




14年11月 怜悧玲瓏 高校数学を天空から俯瞰する




合同式 Mod を応用して京大入試問題を解こう 不定方程式の問題も解説 遊ぶ数学



連立合同式についてです この問題の解き方が分かりません また 逆 Yahoo 知恵袋




22 共通テスト 数学 A 問4 1次不定方程式 合同式 Mod を利用した解法 裏技 数学メモランダム




1次不定方程式の解き方 数学a 整数 東大合格コム




高校数学a 合同式 Mod とは 問題 解説 公式 学校よりわかりやすいサイト




ユークリッドの互除法は無理という人へ 不定方程式は合同式を試してみて 数学のコツ壺 風いま数学協室




60 合同式 演習 連立合同式の解法2 Youtube




記述量を大きく削減する合同式を生徒に紹介しよう 塾講師ステーション情報局




合同式 Mod の問題と使い方を超わかりやすく説明してみた 理系ラボ



1




整数の性質 合同式を利用して1次不定方程式を解こう 日々是鍛錬 ひびこれたんれん




ユークリッドの互除法は無理という人へ 不定方程式は合同式を試してみて 数学のコツ壺 風いま数学協室




初等整数論11 連立合同方程式と中国剰余定理に触れる 数学 整数論 Youtube




数学 Modってなによ 実は便利な合同式を解説 合同方程式も 大学生の勉強部屋




合同式の方程式の解き方 簡単バージョン 錬成会学習塾



合同式を用いた不定方程式の解き方について質問があります チャート Yahoo 知恵袋




整数 不定方程式 定期テストプラス10点 解き方 数学メモランダム




一次合同方程式の解き方詳解 Youtube




高校数学a 合同式 Mod とは 問題 解説 公式 学校よりわかりやすいサイト




14年11月 怜悧玲瓏 高校数学を天空から俯瞰する



不定方程式とは 問題の解き方を種類別にわかりやすく解説 受験辞典




不定方程式 怜悧玲瓏 高校数学を天空から俯瞰する



2




14年11月 怜悧玲瓏 高校数学を天空から俯瞰する



不定方程式とは 問題の解き方を種類別にわかりやすく解説 受験辞典




合同式の性質を使った整数の余りの計算方法 趣味の大学数学




1993東京大学 理 第2問 倍数証明 三項間漸化式 合同式 実験 規則性 マスマス学ぶ




ユークリッドの互除法は無理という人へ 不定方程式は合同式を試してみて 数学のコツ壺 風いま数学協室




特別な合同式を解いてみよう 身勝手な主張




共通テスト前日 一次不定方程式解くのは互除法より合同式のほうが絶対楽 受験生必見 Mp3




合同式の方程式の解き方 簡単バージョン 錬成会学習塾




合同式の意味や Mod の性質 実際の使い方を分かりやすく解説




整数問題へのアプローチ 13 合同式でよくある誤用 問題例 怜悧玲瓏 高校数学を天空から俯瞰する




下線が分かりません 合同式もあまりわかってないので教えてほしいです Clearnote



2
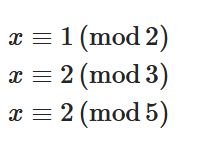



線形合同式の解き方 中国式剰余定理とは何か 趣味の大学数学




合同式の典型問題と考え方 錬成会学習塾




コラム 中国式剰余定理 江戸の数学




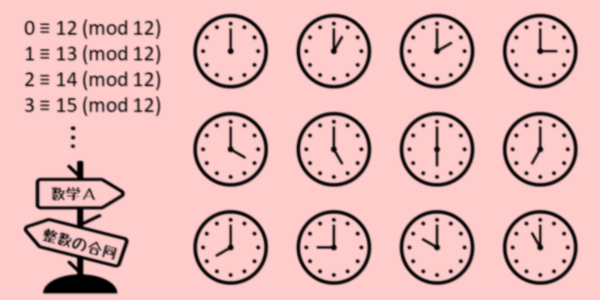
数ia整数 合同式は時計のイメージで理解する 入試問題での使い方 Mm参考書
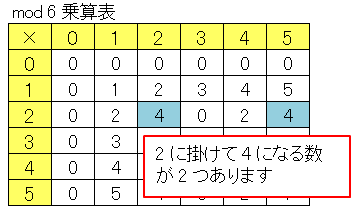



乗算表 乗法表 を用いて一次合同方程式を解く Excel Vba 数学教室



1




翠川からあげ𠷡好 これの合同式 Mod の解き方を教えてくれるお優しい方募集中です T Co Rtyvng3ccz Twitter




合同式 Mod の問題と使い方を超わかりやすく説明してみた 理系ラボ




合同式の方程式の解き方 難しいバージョン 錬成会学習塾




互いに素とは 背理法を使った証明の例題 合同式との関係も合わせて解説 高校生向け受験応援メディア 受験のミカタ




整数 1次不定方程式 合同式 Mod 利用 裏技 数学メモランダム



合同式の証明や問題の解き方を解説 大学受験で使いこなそう Studyplus スタディプラス




合同式の方程式の解き方 難しいバージョン 錬成会学習塾




整数問題へのアプローチ 23 連立合同方程式を優雅に解く 怜悧玲瓏 高校数学を天空から俯瞰する




高校数学a 合同式 Mod とは 問題 解説 公式 学校よりわかりやすいサイト



2




不定方程式を合同式で解く方法詳解 Youtube




裏技 合同式 Mod で一次不定方程式を一瞬で解く方法 Mp3




裏技 合同式 Mod で一次不定方程式を一瞬で解く方法 Mp3




高校数学a 合同式 Mod とは 問題 解説 公式 学校よりわかりやすいサイト




第8章 連立一次合同式




合同式の問題の解き方 合同式の性質の証明 高校生向け受験応援メディア 受験のミカタ




共通テスト前日 一次不定方程式解くのは互除法より合同式のほうが絶対楽 受験生必見 Mp3




合同式 Mod の意味とよく使う6つの性質 高校数学の美しい物語



3




合同式 Mod の問題はこれで解決 一次合同式4タイプを解説します あ いいね




合同式の問題の解き方 合同式の性質の証明 高校生向け受験応援メディア 受験のミカタ




合同式 おいしい数学




合同式 Mod とは 性質の証明や計算問題の解き方 受験辞典



Mod




高校数学a 累乗数の余りと下位桁の数を求める3つの方法 受験の月




差がつく 合同式 基本編 数学の2次試験で合同式を使いこなす マスマス学ぶ



この問題の合同式での解き方教えてください Yahoo 知恵袋
コメント
コメントを投稿